RL Decompiler

Introduction

Decompilation is the process of converting compiled machine code back into readable source code. Decompilers, such as IDA Pro and Ghidra, are used to reverse engineer software into a “C-like pseudocode”, aiding in reverse-engineering. Decompilers are largely based on static analysis and rule-based heuristics. For example, Ghidra has handwritten instructions on how to convert each assembly instruction into a common intermediate representation. From this intermediate representation, a pseudocode is formed. IDA is closed-source, but likely operates the same way. Neither boasts readily compilable source code.

In this post, we explore the use of reinforcement learning to train a LoRA adapter for Qwen2.5-Coder-7B-Instruct, repurposing the model as an end-to-end decompiler for C++. The model will be trained with two goals in mind:

Generate source code that is immediately ready to compile. Generate source code that is as faithful to the original executable as possible. The complete script I use to train the model can be found here.

How reinforcement learning assists with these goals

Decompilation is a translation task, and translation tasks are often trained using cross-entropy loss on a parallel corpus. There are many existing AI decompilers that are trained in this way. However, this does not that the generated code is compilable. With reinforcement learning, we can incentivize the model to generate compilable code by rewarding it for doing so, addressing goal #1.

Qwen Coder is trained on a large corpus of code, and this probably includes some amount of parallel corpora of C++/ASM. In essence, the model already possesses some understanding of the relationship between C++ and assembly. Through reinforcement learning, we are collapsing the search space of possible translations and can address goal #2.

Algorithm details

A key component of reinforcement learning is how we define our rewards. For this experiment, we need to define a metric that captures the quality of a decompilation. An easy metric we can use is Levenshtein distance. Levenshtein distance is the minimum number of single-character edits (insertions, deletions or substitutions) required to change one string into the other (a more robust approach might use a token-wise edit distance).

First, we will generate a target assembly with “Compiler X”, and then measure the Levenshtein distance between the target assembly and the assembly generated by the output of our model compiled with “Compiler X”. In theory, we should be able to achieve a Levenshtein distance of 1, which would indicate that the generated assembly is identical to the original assembly. When the code does not compile, the reward is 0. Note that this does not require any supervision of the source code used to generate the target assembly.

One limitation of this approach is that it requires a specific “Compiler X” to be used across training and inference. However, this can be a strength in reverse engineering contexts where often, the original compiler can be discovered (compiler provenance). If we are able to train the model on a corpus of assembly listings from a single compiler, we could expect the model to very accurately decompile genuine programs from that compiler.

There are several frameworks we can use for reinforcement learning. Let’s use the verl library, which implements Group Relative Policy Optimization (GRPO) and sharded training. For a given sample, GRPO generates several candidate completions, then optimizes the policy to prefer completions within the group that receive comparatively higher rewards. For example, if we prompt Qwen Coder to generate 10 potential decompilations for a given assembly listing, some portion might fail to compile (0 reward) and will be ranked the lowest. Other completions might identify that the assembly implements a certain algorithm and provide a vague implementation. This would be ranked higher than those that fail to compile, but lower than a literal translation that attends to each instruction.

GRPO was initially proposed with a reward model (an LLM judge computes the reward), but for our purposes this is not useful. Thankfully, verl allows us to define a custom reward function. The GRPO algorithm contains two main terms: the reward computed from the current policy and a penalty for deviating too far from the reference policy (i.e the original model):

The penalty is measured by using the KL divergence between the current policy and the reference policy. The influence of the penalty for deviating too far from the reference policy is controlled by tunable coefficient β. If this coefficient is too high, the output distribution will be very similar to the reference policy. If it is too low, the model might deviate too far from the reference policy and show signs of “reward hacking”.

Typically, verl will load a frozen copy of the original model into memory in order to compute the reference policy. It is possible to set β to zero and avoid loading the original model into memory entirely. This means we are losing out on an important regularization term. However, since we are going to train a LoRA adapter, we can add a weight decay term to the optimizer, which apparently regularizes the parameters back to the original model. While these are two different methods of regularization, they seem close enough for our purposes.

Dataset

The source of our training data is Google DeepMind’s code_contests dataset, which is one of the largest datasets of readily compileable code (as far as I’m aware). I created a separate dataset only containing the subset of solutions written in C++ here.

The following python function compiles the code from the dataset into assembly, then splits the assembly into separate functions.

def compile_and_split(sample: dict, *, sample_id: int) -> Optional[Dict[str, str]]:

    flags = [
        "-O2", "-std=c++17",
        # filter out directives and debugging information
        "-fno-verbose-asm", "-fno-asynchronous-unwind-tables",
        "-fno-stack-protector", "-fno-ident", "-g0",
        "-fno-inline-functions", "-fno-inline-functions-called-once",
        "-fno-implicit-templates", "-fno-rtti", "-fno-exceptions",
    ]

    # compile to a human-readable assembly listing
    res = subprocess.run(
        ["g++", *flags, "-x", "c++", "-", "-S", "-o", "-"],
        input=tu.encode(), stdout=subprocess.PIPE, stderr=subprocess.PIPE
    )
    if res.returncode:
        return None
    asm_text = res.stdout.decode("utf-8", "replace")
    asm_text = strip_directives(asm_text)

    # split into functions
    funcs, current, buf = {}, None, []
    for line in asm_text.splitlines(keepends=True):
        # ...

Training

There are many cloud providers offering compute resources, but I chose Modal.com for the $30 of credits it offers in its free tier, which is enough to train this model. Modal provides a verl example that we can adapt to train our model.

Our reward function involves compiling source code, which is rather slow and should be parallelized. In order to parallelize a custom reward function in verl, we need to add a parameter for the reward model in our configuration (despite not actually using a reward model): "reward_model.reward_manager='batch'".

Here is our reward function (simplified):

def reward_diff(solution_strs, ground_truths=None, data_sources=None, abilities=None, reward_models=None, extra_infos=None):
    n_comp = len(solution_strs)
    rewards = []

    no_code = 0
    comp_fail = 0
    empty_funcs = 0

    # Build compile jobs from model completions
    jobs = []
    for idx, completion in enumerate(solution_strs):
        src = extract_code(completion) # expect completions to have a fenced code block
        if src is None:
            no_code += 1
        else:
            jobs.append((idx, src))

    compiled = dispatch_compile_and_split(jobs, max_workers=os.cpu_count(), progress=False)

    for idx in range(n_comp):
        ref_asm = ground_truths[idx if idx < len(ground_truths) else -1]

        # If the completion had no code, reward = 0
        if idx not in compiled:
            rewards.append(0.0)
            continue

        gen_funcs = compiled[idx]
        if gen_funcs is None:
            comp_fail += 1
            rewards.append(0.0)
            continue

        scores = []
        for _, gen_asm in gen_funcs.items():
            dist = Levenshtein.distance(gen_asm, ref_asm)
            norm = max(len(ref_asm), len(gen_asm)) or 1
            scores.append(1.0 - dist / norm)

        if not scores:
            empty_funcs += 1
            rewards.append(0.0)
        else:
            rewards.append(max(scores))

    return rewards

The full script can be found here.

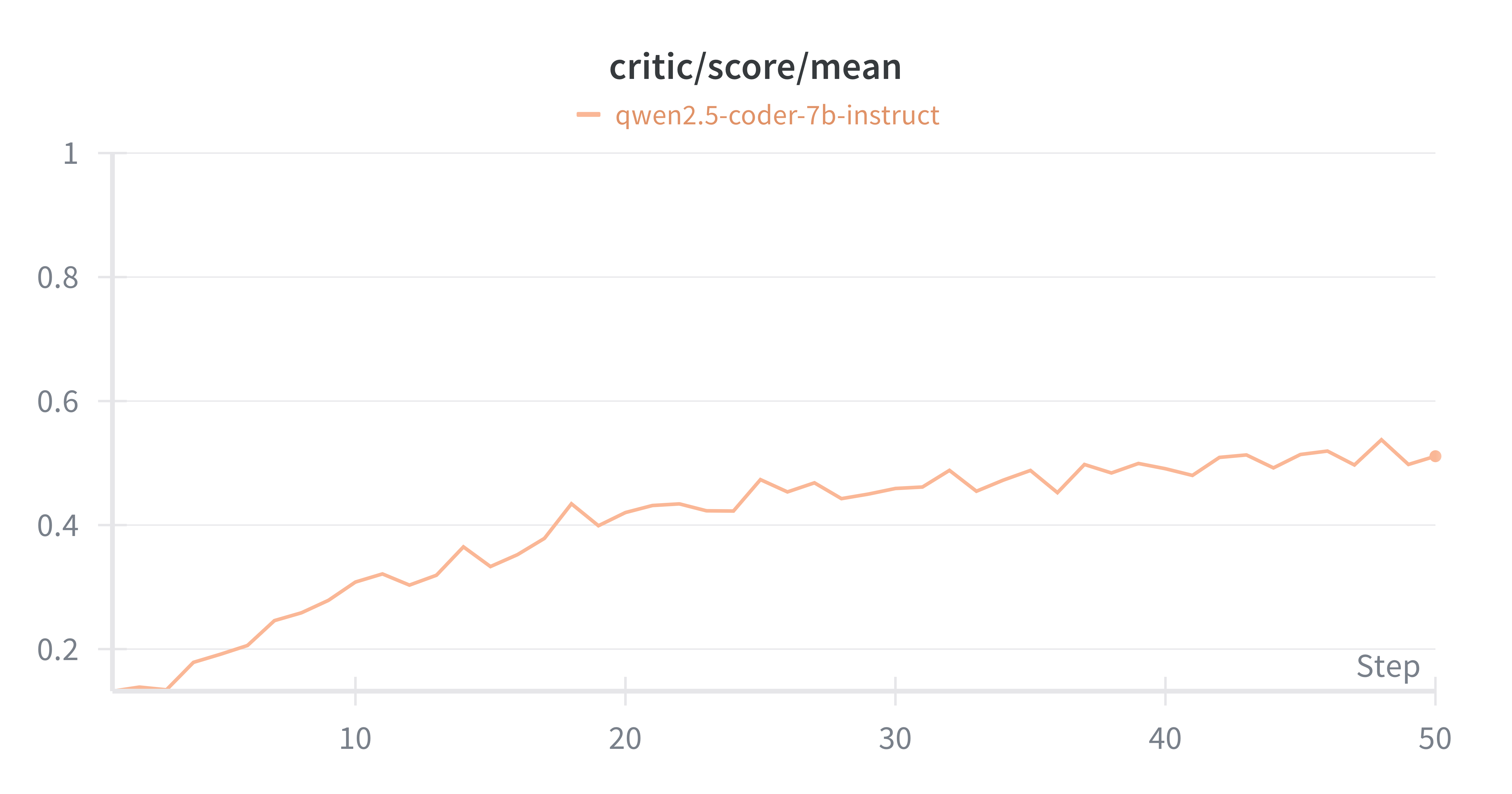
Between the LoRA adapter, and not using reference/reward models (which both need to be loaded into memory), training this model has a very low footprint. The model converges at ~30 steps (6 1/2 hours). Each step processes around 700,000 tokens, so it took around 21 million tokens to converge.

Evaluation

Here is the model output for a snippet of assembly:

******** Original **********

s32 effect_J4_init(u8 data2) {
    WORK_Other * ewk;
    s16 ix;

    if ((ix = pull_effect_work(5)) == -1) {
        return -1;
    }
    
    ewk = (WORK_Other *)frw[ix];
    ewk->wu.be_flag = 1;
    ewk->wu.id = 194;
    ewk->wu.dir_timer = data2;
    ewk->wu.work_id = 16;
    ewk->wu.my_family = 8;
    
    if (data2 != 0xFF) {
        ewk->wu.type = 1;
    }
    
    ewk->wu.my_col_code = 1;
    ewk->wu.my_clear_level = 144;
    return 0;
}

******** Decompiled **********

extern char frw[];

int effect_J4_init(int edi) {
    int result = pull_effect_work(5);
    if (result == -1) {
        return -1;
    }

    int index = result * 1792 + edi;
    frw[index] = 1;
    *(short*)(frw + index + 174) = edi;
    *(int*)(frw + index + 6) = 12714000;
    *(short*)(frw + index + 678) = 8;

    if (edi!= -1) {
        frw[index + 4] = 1;
    }

    *(short*)(frw + index + 674) = 1;
    *(short*)(frw + index + 686) = 144;

    return 0;
}

We see that our model successfully translated important parts of the compiled program back into C++. Access to data structures has been translated into pointer arithmetic, which might be a symptom of reward hacking. There is no incentive for the model to generate proper classes or structs or penalty for writing “unusual” code.

Let’s do a quick comparison between our model and GPT 4.1.

client = OpenAI()

def gen_gpt5(prompt: str) -> str:
    messages = [
        {"role": "system", "content": "You are a precise C++ decompiler. Return only a single fenced ```cpp code block."},
        {"role": "user", "content": prompt},
    ]
    resp = client.chat.completions.create(
        model=GPT5_MODEL,
        messages=messages,
        # temperature=TEMPERATURE,
        max_completion_tokens=MAX_NEW_TOKENS,
    )
    return resp

# Build prompts and refs
prompts = df_val["prompt"].tolist()
refs    = df_val["ground_truth"].tolist()

# GPT-4.1
gpt4_comps = generate_gpt4(prompts)
gpt4_rewards, gpt4_metadata = compute_rewards(gpt4_comps, refs)
gpt4_mean = float(np.mean(gpt4_rewards)) if gpt4_rewards else 0.0

# Local model
tok, mdl = load_qwenrl_model()
local_comps = generate_qwenrl(prompts, tok, mdl)
local_rewards, qwenrl_metadata = compute_rewards(local_comps, refs)
local_mean = float(np.mean(local_rewards)) if local_rewards else 0.0

Comparing the results, we see that our model is able to consistently produce source code that compiles. Of the code that does successfully compile, our model increases the Levenshtein score by 19.6% when compared to the output of GPT 4.1.

==== Evaluation Summary ====
Samples: 39
qwen: mean reward@1 = 0.0604 | no_code: 28, comp_fail: 1, empty_funcs: 0, n: 39
qwen-ours: mean reward@1 = 0.3946 | no_code: 7, comp_fail: 0
gpt-4.1: mean reward@1 = 0.3298 | no_code: 17, comp_fail: 2

Conclusion

This was a simple experiment to show how reinforcement learning can leverage LLMs for decompilation tasks. There are many improvements that can be made, such as pretraining on a C++/ASM corpus, and incentivizing struct generation or the use of high-level design patterns such as stdlib classes (low-hanging fruit, if someone wants to test this). Another task would be to give the model partial C++ implementation, and ask it to “improve the score”, potentially allowing the model to iterate on its own outputs in an agentic manner.